Resúmenes numéricos

Ingeniería de Datos Aplicado a la Estadística, PEUCD 2025

Víctor Fuentes Campos
vfuentes@ipe.org.pe

2025-08-07

Medidas de localización: media, mediana y moda

Medidas del centro: media

La media aritmética es la suma de todos los valores dividida por el número total de observaciones. Es sensible a los valores atípicos, ya que estos pueden influir significativamente en su valor.

  • Ventaja: Utiliza toda la información de los datos.

  • Desventaja: Afectada por valores extremos (outliers).

Medidas del centro: media

[1] 56.4

Medidas del centro: media

[1] 64.90909

Medidas del centro: mediana

Otra medida de centro es la mediana. La mediana es el valor en el que el 50 % de los datos es inferior a ella y el 50 % es superior. Podemos calcularla ordenando todos los puntos de datos y tomando el del medio.

  • Ventaja: Resistente a los valores extremos.

  • Desventaja: No utiliza toda la información de los datos.

Medidas del centro: mediana

[1] 56.5

Medidas del centro: mediana

[1] 58

Medidas del centro: moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. En distribuciones multimodales puede haber más de una moda, o no existir si todos los valores son únicos.

  • Ventaja: Útil para datos categóricos.
  • Desventaja: Puede no ser única o no existir en datos continuos.

La moda se utiliza a menudo para variables categóricas, ya que las variables categóricas pueden estar desordenadas y, a menudo, no tienen una representación numérica inherente.

Medidas del centro: moda

[1] 50

Medidas del centro: moda

Media vs. Mediana vs. Moda

Media vs. Mediana vs. Moda: Con outlier

Medidas de dispersión: rango, desviación estándar, varianza

Medidas del dispersión: rango

Para encontrar el rango, solo basta restar el valor mínimo de datos del valor máximo de datos. Algunas personas dan el rango simplemente enumerando el valor mínimo de datos y el valor máximo de datos. Sin embargo, para los estadísticos el rango es un solo número.

[1] 50
[1] 62
[1] 12

Medidas del dispersión: varianza

Mide la distancia promedio desde cada punto de datos hasta la media de los datos. Para ello:

  • Calculamos la distancia entre cada punto y la media

  • Luego elevamos al cuadrado cada distancia y luego las sumamos todas.

  • Por último, dividimos la suma de las distancias al cuadrado entre el número de puntos de datos

Es importante tener en cuenta que las unidades de varianza son el cuadrado. Cuanto mayor sea la varianza, más dispersos estarán los datos.

Medidas del dispersión: varianza

[1] 14.67778

Medidas del dispersión: desviación estándar

Mide el promedio de las distancias de cada punto respecto a la media. Una desviación estándar alta indica que los datos están muy dispersos respecto a la media, y una baja indica que están más cerca de la media.

Medidas del dispersión: desviación estándar

Medidas de distribución: cuartiles y percentiles

Medidas de distribución: cuartiles

Dividen el conjunto de datos en partes iguales. Los cuartiles dividen los datos en cuatro partes (cuartiles), mientras que los percentiles dividen los datos en cien partes.

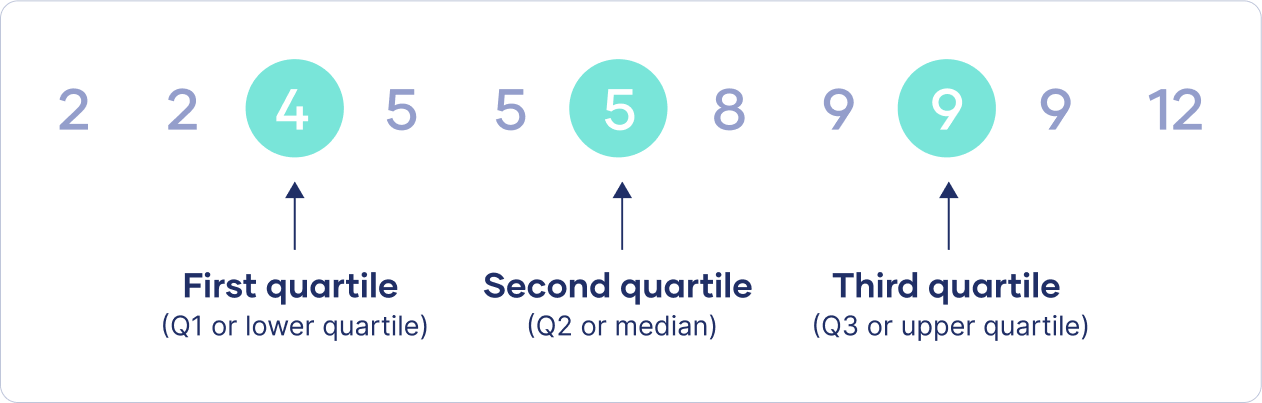
El primer cuartil (Q1) es el valor debajo del cual se encuentra el 25% de los datos, el segundo cuartil (Q2) es la mediana, y el tercer cuartil (Q3) es el valor debajo del cual se encuentra el 75% de los datos.

Medidas de distribución: cuartiles

Banner

Medidas de distribución: percentiles

El percentil es una medida estadística que divide una serie de datos ordenados de menor a mayor en cien partes iguales. Se trata de un indicador que busca mostrar la proporción de la serie de datos que queda por debajo de su valor.

Medidas de distribución: percentiles

Banner

Medidas de forma: asimetría y curtosis

Medidas de forma: asimetría

El coeficiente de asimetría mide la simetría de la distribución. Una asimetría cercana a 0 indica una distribución simétrica. Un valor positivo indica que los datos tienen una cola más larga a la derecha, mientras que un valor negativo indica lo contrario.

Medidas de forma: asimetría

Medidas de forma: cuartiles

Banner

Medidas de forma: curtosis

La curtosis mide el “apuntalamiento” de la distribución. Una curtosis positiva indica colas más pesadas que una distribución normal, mientras que una curtosis negativa indica colas más ligeras.

Medidas de forma: curtosis

Aplicación en R

Perú: El mercado de autos usados

# install.packages("readr")

library(readr)
url_base <-
  "https://raw.githubusercontent.com/vfuentesc/databases/refs/heads/main/"
archivo <- "neoauto_202409.csv"
url_archivo <- paste0(url_base,  archivo)
datos <- read_csv(url_archivo, locale = locale(encoding = "UTF-8"))

Perú: El mercado de autos usados

# install.packages("devtools")
# devtools::install_github("ropensci/skimr")

library(skimr)
skim(datos)
Data summary
Name datos
Number of rows 4041
Number of columns 23
_______________________
Column type frequency:
character 13
logical 2
numeric 8
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
item_name 0 1.00 9 44 0 2209 0
item_category 0 1.00 5 5 0 1 0
item_category_2 0 1.00 4 14 0 7 0
item_brand 0 1.00 2 14 0 73 0
item_transmission 0 1.00 8 23 0 3 0
item_fuel 0 1.00 3 16 0 9 0
item_location_city 0 1.00 3 12 0 20 0
item_location_province 0 1.00 3 16 0 38 0
item_tag 2435 0.40 6 22 0 24 0
item_advertiser 0 1.00 3 59 0 2536 0
item_financed_by 781 0.81 9 9 0 1 0
item_publication_slug 0 1.00 28 63 0 4041 0
item_publication_type 0 1.00 6 9 0 4 0

Variable type: logical

skim_variable n_missing complete_rate mean count
item_credit 0 1 0.81 TRU: 3260, FAL: 781
item_verified 0 1 0.19 FAL: 3281, TRU: 760

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
value 0 1.00 21078.80 16772.82 0 11900 17500 25900 345000 ▇▁▁▁▁
item_id 0 1.00 1795121.63 27339.16 1253542 1798670 1803888 1806192 1807420 ▁▁▁▁▇
item_price 0 1.00 22032.99 18258.95 0 12500 17900 26500 345000 ▇▁▁▁▁
item_km 0 1.00 59136.26 53023.62 0 25000 50736 80000 975581 ▇▁▁▁▁
item_year 0 1.00 2017.20 6.22 1955 2015 2018 2021 2025 ▁▁▁▁▇
price 0 1.00 22032.99 18258.95 0 12500 17900 26500 345000 ▇▁▁▁▁
santander_price 2964 0.27 20647.53 11407.20 7000 12500 17500 25500 76500 ▇▃▁▁▁
item_publication_type_Id 0 1.00 26.30 1.24 25 25 26 28 28 ▇▃▁▃▅

Precio promedio de todos los autos

media <- mean(datos$item_price, na.rm = TRUE)
mediana <- median(datos$item_price, na.rm = TRUE)
moda <-  as.numeric(names(sort(table(datos$item_price),
                                       decreasing = TRUE)[1]))
print(media)
[1] 22032.99
print(mediana)
[1] 17900
print(moda)
[1] 18500

¿Es una medida adecuada? ¿Qué opinan?

Precio promedio según categoría

# install.packages("dplyr")
library(dplyr)

ggplot(datos, aes(x = item_category_2, y = value, fill = item_category_2)) +
  geom_boxplot() +
  stat_summary(fun = median, geom = "point", shape = 20, size = 3, color = "red") +
  labs(title = "Boxplot del Precio por Categoría de Auto",
       x = "Categoría del Auto",
       y = "Precio") +
  theme_minimal() +
  scale_fill_brewer(palette = "Set3") +         ##agregamos colores
  scale_y_continuous(labels = scales::comma)    ## para que se muestren los precios correctamente en el eje "Y"

Precio promedio según categoría

¿Sería correcto hallar la media de todos los autos sin considerar el tipo de auto?

Media, mediana y moda

precio_descripcion <- datos |> 
  group_by(item_category_2) |> 
  summarise(
    mean_price = mean(item_price, na.rm = TRUE),
    median_price = median(item_price, na.rm = TRUE),
    mode_price = as.numeric(names(sort(table(item_price),
                                       decreasing = TRUE)[1]))
  )

# Mostrar los resultados al usuario
print(precio_descripcion)

Media, mediana y moda

# A tibble: 7 × 4
  item_category_2 mean_price median_price mode_price
  <chr>                <dbl>        <dbl>      <dbl>
1 Camionetas Suv      24990.        20500      17500
2 Deportivo           34451.        21500          0
3 Hatchback           14584.        12800      10500
4 Pick Up             26024.        24900      20000
5 Sedan               15670.        12750      10000
6 Station Wagon        5295.         5000       2800
7 Vans                13482.        11950      11000

Media, mediana y moda para las ‘Pick-Up’

Media, mediana y moda para las ‘Pick-Up’ sin valores extremos

Coeficiente de asimetría y curtosis para ‘Pick-Up’ con outliers

[1] "Coeficiente de asimetría:  5.56"

Coeficiente de asimetría y curtosis para ‘Pick-Up’ sin outliers

[1] "Asimetría: 5.55954864405599"
[1] "Curtosis: 60.5836866579883"