Resúmenes gráficos

Ingeniería de Datos Aplicado a la Estadística, PEUCD 2025

Víctor Fuentes Campos

vfuentes@ipe.org.pe

2025-08-12

Las clásicas barras

Gráficos de barras

Los gráficos de barras son efectivos para visualizar la frecuencia (absoluta o relativa) de cada categoría.

Gráficos de barras

Gráficos de barras apiladas

Gráficos de barras agrupadas

Gráficos de barras horizontales

Gráficos de barras horizontales apiladas

Gráficos de barras flechas horizontales

Pasteles, donas, voronoi y mapas de árbol

Gráficos de pasteles

Los gráficos de pastel, donas, voronoi o mapas de árbol son una forma visual de representar cómo se distribuyen las categorías de una variable en proporciones relativas a un todo.

Gráficos de pastel

Gráficos de donas

Gráficos de voronoi

Gráficos de ¿voronoi?

Gráficos de mapa de árboles

PS: Probablemente una mala opción para un comparativo

Líneas y áreas

Gráficos de líneas y áreas

Útiles para mostrar tendencias o patrones a lo largo del tiempo o en relación con una variable continua.

Gráficos de líneas

Gráficos de múltiples líneas

Gráficos de líneas barras

Gráficos de líneas y áreas

Gráficos de áreas

Histogramas y cajas

Histogramas

Un histograma representa la distribución de un conjunto de datos numéricos. Los datos se agrupan en intervalos (o bins), y la altura de cada barra del histograma indica la frecuencia de los datos dentro de ese intervalo.

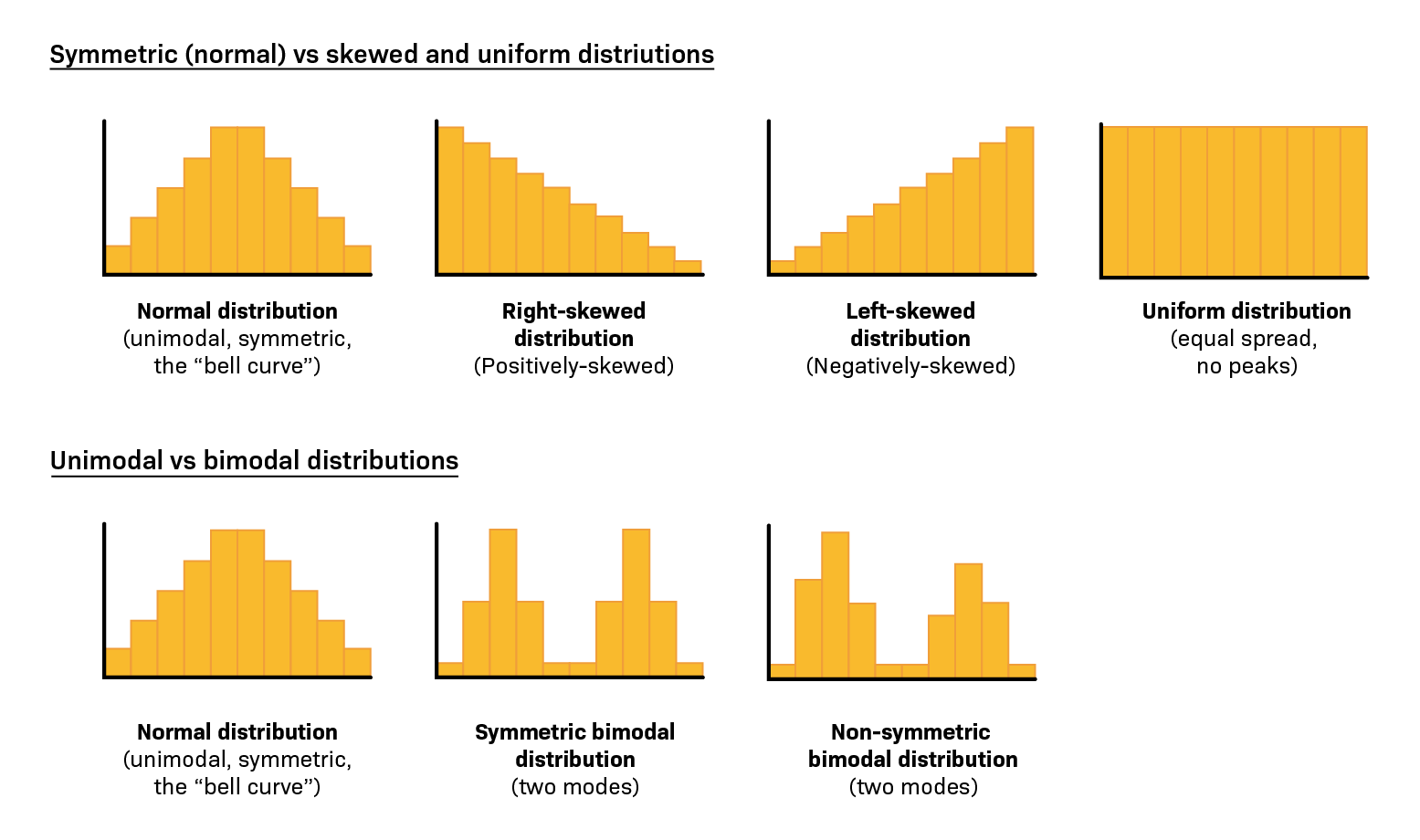
Simetría: Tiene una forma similar en ambos lados del centro.
Sesgo (skewness): Si una cola de la distribución está más hacia un lado.
Modas: Picos o concentraciones de datos indican dónde se agrupan los valores.

Histograma y tipos de distribuciones

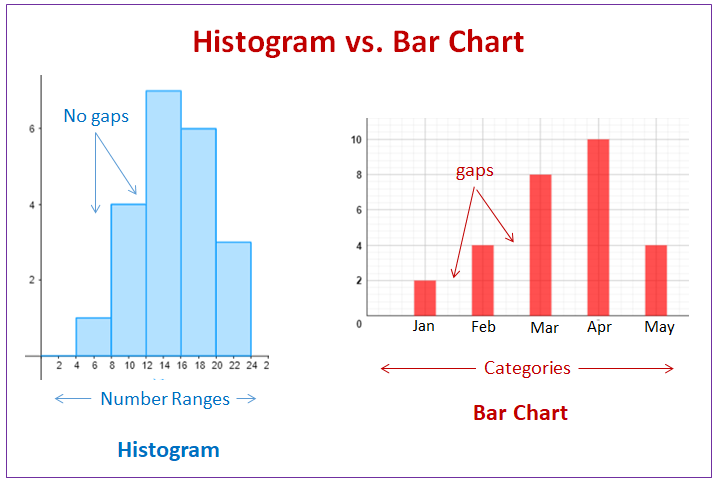
Histograma vs Barras

Histograma

Elección del número de intervalos (bins)

El número de intervalos (bins) en un histograma afecta directamente a cómo se interpreta la forma de la distribución. Un número pequeño de intervalos puede ocultar detalles importantes, mientras que un número excesivo puede hacer que la distribución parezca “ruidosa”.

Elección del número de intervalos (bins)

Reglas para elegir el número de intervalos:

Regla de Sturges: Una fórmula simple basada en el logaritmo del número de observaciones.
Regla de Freedman-Diaconis: Se basa en el rango intercuartil (IQR) y es más robusta cuando existen outliers.
Selección automática: Muchos softwares seleccionan automáticamente el número de bins según la distribución de los datos.

Elección del número de intervalos (bins)

Regla de Sturges: utiliza el logaritmo del tamaño de la muestra para calcular el número de bins. La fórmula es la siguiente: \[\text{bins} = \log_2(n) + 1\]
Regla de Freedman-Diaconis: usa el rango intercuartil (IQR) y es más robusta cuando hay outliers: \[\text{bin width} = 2 \cdot \frac{\text{IQR}}{n^{1/3}}\]

Una vez calculado el ancho del bin, el número de bins se obtiene dividiendo el rango de los datos entre el ancho del bin
Selección automática: Selección de los softwares en función de la densidad de los datos y otros factores para ajustar visualmente la agrupación

Elección del número de intervalos (bins): comparativo

¿Histogramas en las cámaras?

Cajas o Boxplot

El gráfico de caja es una representación estadística diseñada para destacar aspectos clave de la distribución en una o más series de datos cuantitativos, facilitando la identificación de la mediana, los cuartiles y los valores atípicos.

Boxplot

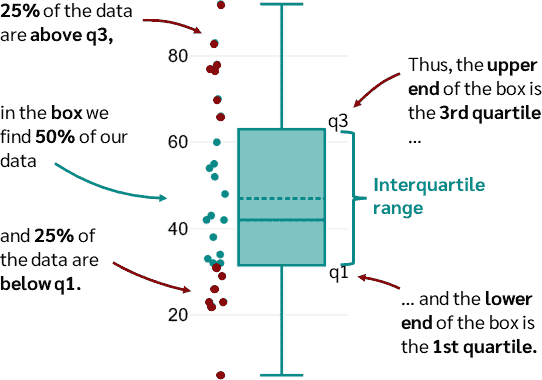
Boxplot: Mediana o Q2

La mediana es el valor central que divide la serie de datos en dos partes iguales. En el boxplot, se representa como una línea dentro de la caja.

[1] 49.94695

Boxplot: RIQ (IQR)

El IQR muestra la distancia o diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1), y representa el rango donde se encuentra el 50% central de los datos, mostrando la dispersión de la distribución. Para calcularlo usaremos quantile().

Q1: 43.26553

Q3: 56.78582

IQR: 13.5203

Boxplot: Bigotes

Los bigotes muestran los valores más alejados del centro que no son considerados outliers. Los bigotes representan los rangos del 25 % de valores de datos de la parte inferior y el 25 % de la parte inferior.

Boxplot: Cuartiles (Q1 y Q3)

El primer cuartil (Q1) es el valor por debajo del cual se encuentra el 25% de los datos, mientras que el tercer cuartil (Q3) es el valor por debajo del cual se encuentra el 75% de los datos. Estos definen los bordes de la caja en el boxplot.

Boxplot con outliers

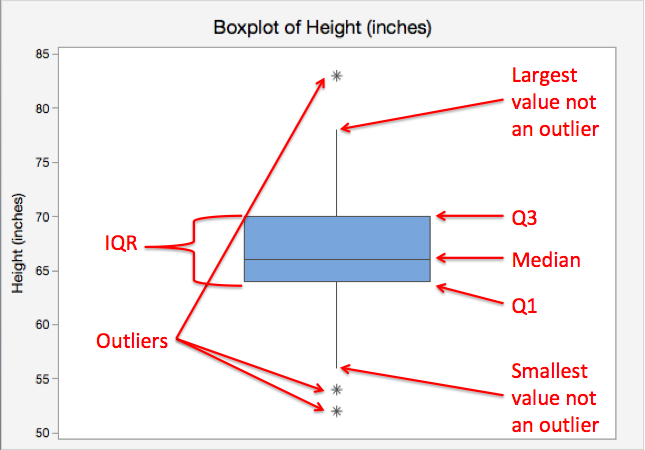
Boxplot: Outliers

Los outliers son puntos fuera de los bigotes y se consideran valores anómalos. Son útiles para identificar variaciones extremas en los datos.

Boxplot: Resumen

Los outliers son puntos fuera de los bigotes y se consideran valores anómalos. Son útiles para identificar variaciones extremas en los datos.